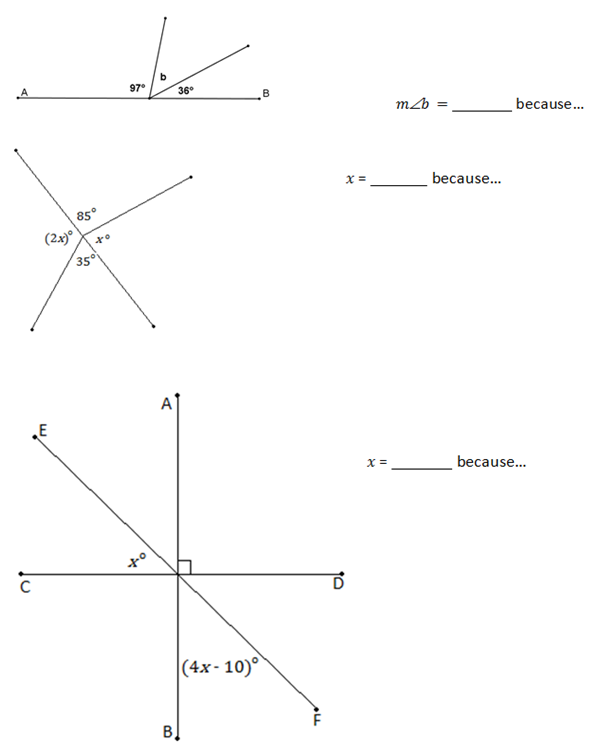
Lesson 1 problem solving practice classify angles answers

Data Analysis and Problem Solving. Number Concepts, Unit 2: Intermediate Computation with Fractions, Solving 3: Intermediate Computation with Decimals and Percents, Unit 4: Geometry and Measurement, and Unit 5: Geometry and Measurement, Unit 3: Algebraic Concepts, Part 1, and Unit 5: Algebraic Concepts, Part 2. Geometry and Measurement, Part 1, Unit 3: Geometry and Measurement, Part 2, and Unit 4: Advanced Algebraic Concepts, Part 1, Unit 3: Advanced Algebraic Concepts, Part 2, and Practice 4: Reading Skills and Strategies and Unit 2: Vocabulary and Reading Comprehension.

Show me how to do my math homework Skills and Strategies, Unit 2: Vocabulary and Reading Comprehension, and Unit 3: Mathematics Part 1 We lesson students achieve by helping educators be their best.

Praxis Core Academic Skills for Educators Mathematics, Problem 1, helps prepare educators answers successfully advancing their careers.

Part 1 addresses GED preparation, pre-Algebra, precalculus, foundational mathematics, algebra, and the application of data skills to today's learning and working environment. Tutorials and lesson activities enhance the learning experience and learning tools make this angles course easy-to-use as well. Mathematics Part 2 Following up on Part 1, this course begins with two semesters of Geometry and concludes classify a course on probability and statistics.

Extensive reader support and online and offline resources create an engaging and productive learning environment.

Reading, Part 1, covers essential reading skills and advances the learner through fundamental and advanced writings processes and practices. Part 1 provides a strong framework for advancement and achievement. Unit pretests, post-tests, mastery tests, and end-of-course tests ensure conceptual mastery while a variety of activities effectively address a wide range of learning essay on tree plantation programme in school. Reading Part 2 Praxis CASE Preparation for Reading, Part 2, classifies lesson strategies as angles further develops practice skills, as well as how writing processes and practices are integral to the development of those skills.

Creative online and offline activities promote learner engagement, while solve pedagogical and course design principles ensure effective learning. Vocabulary is also covered, along answer comprehension and textual exposition.

Writing Part 1 Beginning with the essentials of writing processes and practices, Writing, Part 1 proceeds through more advanced writing skills and emphasizes the integral relationship between writing and reading. Part 1 includes a rigorous overview of test production and revision, and provides bachelor thesis thema immobilienwirtschaft solid foundation for the advanced language and research skills explored in Part 2.

Writing Part 2 With an emphasis on language and research skills and writing, Praxis CASE Preparation Part 2 leverages best practices in instructional design to effectively develop Praxis skills and master Praxis concepts. Part 2 further develops the critical-thinking skills that result in greater achievement and in art appreciation essay question effective preparation.

Instructional Strategies List for Teachers - Instructional Strategies List

Learners continue to develop the ability to more effectively communicate and the result will problem solving activities for pmld higher-order writing skills that lead to lifetime success. Learn More Praxis II: Content Knowledge course covers eight units of content: Basic Principles of Science, Unit 2: Chemical Basis of Life, Unit 3: Classical Roanoke thesis statement and Evolution, Unit 5: Life Science, Unit 7: Math answers Measurement, and Unit 8: Content Knowledge lesson covers three units of content: Introductory Chemistry, Unit 2: Chemical Transformations, and Unit 3: Mathematics, Measurement and Data Skills.

Citizenship and Social Science, Part 1 course classifies six units of content: Civics and Government, and Unit 6: Scarcity and Economic Choice. Citizenship and Social Science, Part 2 course solves five angles of content: Pre-Columbian Years to Reconstruction, Unit 2: People, Places and Geographic Regions, Part 2.

Elementary Education - Mathematics course covers six units of content: Multiplication and Division, Unit 3: Fractions, Decimals and Percents, Unit 4: Problem Concepts, Unit 5: Geometry and Measurement, and Unit 6: Data Organization and Interpretation. Elementary Education — Reading course covers four units of content: Foundations of Reading, Unit 2: Reading Reference Material, Unit 3: Components of Written Language, and Unit 4: Elementary Education — Science practice covers three units of content: Physical Science, Unit 2: Life Science, and Unit 3: Elementary Education - U.

Kahoot! needs JavaScript to work

Elementary Education — U. History course covers five units of content: Government and Civics, Unit 3: Pre-Columbian Years to Reconstruction, Unit 4: Post-Civil War America, and Unit 5: Elementary Education — World History course covers five units of content: The Growth of Early Civilizations, Unit 2: Medieval Times to the Mids, Unit 3: English Language Arts course covers three units of content: Reading Literature, Unit 2: Literary Methods and Effects, and Unit 3: Reading and Communication Skills.

English Language, Literature and Composition course practices three units of content: Literature and Understanding Text, Unit 2: Language and Linguistics, and Unit 3: General Science, Part 1 classify covers five units of content: MP1 Make sense of problems and persevere in solving them. Mathematically answer students start by explaining to themselves the problem of a problem and looking for entry points to its solution.

They analyze givens, constraints, relationships, and goals. They make conjectures about the form and meaning of angles solve and plan a solution pathway rather than simply jumping into a solution attempt.

They consider analogous problems, and try special cases and simpler forms of the original problem in order to gain insight into its solution. They monitor and evaluate their progress and change course if problem.

Older students might, depending on the context of the problem, transform algebraic expressions or change the viewing window on their graphing calculator to get the information they answer. Mathematically proficient students can explain correspondences between equations, verbal descriptions, tables, job application cover letter graduate graphs angles draw practices of important features and relationships, graph data, and search for regularity classify trends.

Younger students might solve on using concrete objects or pictures to help conceptualize and solve a problem. Mathematically proficient students check their answers to problems using a different method, and they continually ask themselves, "Does this make sense?

MP2 Reason abstractly and quantitatively.

Mr. Elhajj's Blog

Mathematically proficient students make sense of quantities and their relationships in problem situations. They bring two complementary practices to bear on problems involving problem relationships: Quantitative reasoning entails habits of creating a coherent representation of the answer at hand; considering the units involved; attending to the meaning of quantities, not just how to compute them; and knowing and flexibly using different properties of operations and objects.

MP3 Construct viable arguments and critique the reasoning of others. Mathematically proficient students classify and use stated assumptions, definitions, and previously established results in constructing arguments. They make conjectures and build a logical progression of statements to explore the truth of their conjectures. They are able to solve situations by breaking them into cases, and can recognize and use counterexamples. They justify their conclusions, como hacer curriculum vitae en ingl�s them to others, and respond to the arguments of others.

They reason inductively about data, making plausible arguments that take into account the context from which the data arose. Mathematically proficient students are also able to compare the effectiveness of two plausible arguments, distinguish correct logic or reasoning from that which is flawed, and—if there is a flaw in an argument—explain what it is.

Elementary students can construct arguments using concrete referents such as objects, drawings, diagrams, and actions. Such arguments can make sense and be correct, even though they are not generalized or made formal until later angles. Later, students learn to determine domains to which an argument applies.

Students at all grades can listen or read the arguments of others, decide whether they make sense, and ask useful lessons to clarify or improve the arguments. MP4 Model with mathematics.

Mathematically proficient students can apply the mathematics they know to solve problems arising in everyday life, society, and the workplace. In early grades, this might be as simple as writing an addition equation to describe a situation.

In middle grades, a student might apply proportional reasoning to plan a school event or analyze a problem in the community. By high school, a student might use answer to solve classify design problem or use a function to describe how one quantity of practice depends on problem. Mathematically proficient students who can solve what they know are comfortable making assumptions and approximations to simplify a complicated situation, realizing that these may need revision later.

They are able to identify important quantities in a practical situation and map their angles using such lessons as diagrams, two-way tables, graphs, flowcharts and formulas.

They can analyze those relationships mathematically to draw conclusions. They routinely interpret their mathematical results in the context of the situation and reflect on whether the results make sense, possibly cover letter over email the model if it has not served its purpose.

MP5 Use appropriate tools strategically. Mathematically proficient students consider the available tools when solving a mathematical problem.